| 本章节我们将介绍如何用
PyTorch 实现一个简单的前馈神经网络,完成一个二分类任务。
以下实例展示了如何使用 PyTorch 实现一个简单的神经网络进行二分类任务训练。
网络结构包括输入层、隐藏层和输出层,使用了 ReLU 激活函数和
Sigmoid 激活函数。
采用了均方误差损失函数和随机梯度下降优化器。
训练过程是通过前向传播、计算损失、反向传播和参数更新来逐步调整模型参数。
|
#
导入PyTorch库
import
torch
import
torch.nn
as
nn
# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in,
n_h,
n_out,
batch_size =
10,
5,
1,
10
# 创建虚拟输入数据和目标数据
x =
torch.randn(batch_size,
n_in)
# 随机生成输入数据
y =
torch.tensor([[1.0],
[0.0],
[0.0],
[1.0],
[1.0],
[1.0],
[0.0],
[0.0],
[1.0],
[1.0]])
# 目标输出数据
# 创建顺序模型,包含线性层、ReLU激活函数和Sigmoid激活函数
model =
nn.Sequential(
nn.Linear(n_in,
n_h),
# 输入层到隐藏层的线性变换
nn.ReLU(),
#
隐藏层的ReLU激活函数
nn.Linear(n_h,
n_out),
# 隐藏层到输出层的线性变换
nn.Sigmoid()
#
输出层的Sigmoid激活函数
)
# 定义均方误差损失函数和随机梯度下降优化器
criterion =
torch.nn.MSELoss()
optimizer =
torch.optim.SGD(model.parameters(),
lr=0.01)
# 学习率为0.01
# 执行梯度下降算法进行模型训练
for
epoch in
range(50):
# 迭代50次
y_pred =
model(x)
# 前向传播,计算预测值
loss =
criterion(y_pred,
y)
# 计算损失
print('epoch:
',
epoch,
'loss: ',
loss.item())
# 打印损失值
optimizer.zero_grad()
# 清零梯度
loss.backward()
# 反向传播,计算梯度
optimizer.step()
# 更新模型参数
|
输出结果类似如下:
epoch: 0 loss: 0.2591968774795532
epoch: 1 loss: 0.25902628898620605
epoch: 2 loss: 0.25885599851608276
epoch: 3 loss: 0.25868603587150574
epoch: 4 loss: 0.25851646065711975
...
|
定义网络参数:
n_in, n_h, n_out, batch_size = 10, 5, 1, 10
|
- n_in:输入层大小为 10,即每个数据点有 10 个特征。
- n_h:隐藏层大小为 5,即隐藏层包含 5 个神经元。
- n_out:输出层大小为 1,即输出一个标量,表示二分类结果(0 或 1)。
- batch_size:每个批次包含 10 个样本。
生成输入数据和目标数据:
x = torch.randn(batch_size, n_in) # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0],
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]]) # 目标输出数据
|
- x:随机生成一个形状为 (10, 10) 的输入数据矩阵,表示 10 个样本,每个样本有
10 个特征。
- y:目标输出数据(标签),表示每个输入样本的类别标签(0 或 1),是一个 10×1
的张量。
定义神经网络模型:
model = nn.Sequential(
nn.Linear(n_in, n_h), # 输入层到隐藏层的线性变换
nn.ReLU(), # 隐藏层的ReLU激活函数
nn.Linear(n_h, n_out), # 隐藏层到输出层的线性变换
nn.Sigmoid() # 输出层的Sigmoid激活函数
)
|
nn.Sequential 用于按顺序定义网络层。
- nn.Linear(n_in, n_h):定义输入层到隐藏层的线性变换,输入特征是
10 个,隐藏层有 5 个神经元。
- nn.ReLU():在隐藏层后添加 ReLU 激活函数,增加非线性。
- nn.Linear(n_h, n_out):定义隐藏层到输出层的线性变换,输出为
1 个神经元。
- nn.Sigmoid():输出层使用 Sigmoid 激活函数,将结果映射到 0
到 1 之间,用于二分类任务。
定义损失函数和优化器:
criterion = torch.nn.MSELoss() # 使用均方误差损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 使用随机梯度下降优化器,学习率为 0.01
|
训练循环:
for epoch in range(50): # 训练50轮
y_pred = model(x) # 前向传播,计算预测值
loss = criterion(y_pred, y) # 计算损失
print('epoch: ', epoch, 'loss: ', loss.item()) # 打印损失值
optimizer.zero_grad() # 清零梯度
loss.backward() # 反向传播,计算梯度
optimizer.step() # 更新模型参数
|
- for epoch in range(50):进行 50 次训练迭代。
- y_pred = model(x):进行前向传播,使用当前模型参数计算输入数据 x
的预测值。
- loss = criterion(y_pred, y):计算预测值和目标值 y 之间的损失。
- optimizer.zero_grad():清除上一轮训练时的梯度值。
- loss.backward():反向传播,计算损失函数相对于模型参数的梯度。
- optimizer.step():根据计算出的梯度更新模型参数。
可视化代码:
|
import
torch
import
torch.nn
as
nn
import
matplotlib.pyplot
as
plt
# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in,
n_h,
n_out,
batch_size =
10,
5,
1,
10
# 创建虚拟输入数据和目标数据
x =
torch.randn(batch_size,
n_in)
# 随机生成输入数据
y =
torch.tensor([[1.0],
[0.0],
[0.0],
[1.0],
[1.0],
[1.0],
[0.0],
[0.0],
[1.0],
[1.0]])
# 目标输出数据
# 创建顺序模型,包含线性层、ReLU激活函数和Sigmoid激活函数
model =
nn.Sequential(
nn.Linear(n_in,
n_h),
# 输入层到隐藏层的线性变换
nn.ReLU(),
#
隐藏层的ReLU激活函数
nn.Linear(n_h,
n_out),
# 隐藏层到输出层的线性变换
nn.Sigmoid()
#
输出层的Sigmoid激活函数
)
# 定义均方误差损失函数和随机梯度下降优化器
criterion =
torch.nn.MSELoss()
optimizer =
torch.optim.SGD(model.parameters(),
lr=0.01)
# 学习率为0.01
# 用于存储每轮的损失值
losses =
[]
# 执行梯度下降算法进行模型训练
for
epoch in
range(50):
# 迭代50次
y_pred =
model(x)
# 前向传播,计算预测值
loss =
criterion(y_pred,
y)
# 计算损失
losses.append(loss.item())
# 记录损失值
print(f'Epoch
[{epoch+1}/50], Loss: {loss.item():.4f}')
# 打印损失值
optimizer.zero_grad()
# 清零梯度
loss.backward()
# 反向传播,计算梯度
optimizer.step()
# 更新模型参数
# 可视化损失变化曲线
plt.figure(figsize=(8,
5))
plt.plot(range(1,
51),
losses,
label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training
Loss Over Epochs')
plt.legend()
plt.grid()
plt.show()
# 可视化预测结果与实际目标值对比
y_pred_final =
model(x).detach().numpy()
# 最终预测值
y_actual =
y.numpy()
# 实际值
plt.figure(figsize=(8,
5))
plt.plot(range(1,
batch_size + 1),
y_actual,
'o-',
label='Actual',
color='blue')
plt.plot(range(1,
batch_size + 1),
y_pred_final,
'x--',
label='Predicted',
color='red')
plt.xlabel('Sample
Index')
plt.ylabel('Value')
plt.title('Actual
vs Predicted Values')
plt.legend()
plt.grid()
plt.show()
|
显示如下所示:

另外一个实例
我们假设有一个二维数据集,目标是根据点的位置将它们分类到两个类别中(例如,红色和蓝色点)。
以下实例展示了如何使用神经网络完成简单的二分类任务,为更复杂的任务奠定了基础,通过 PyTorch
的模块化接口,神经网络的构建、训练和可视化都非常直观。
1、数据准备
首先,我们生成一些简单的二维数据:
|
import
torch
import
torch.nn
as
nn
import
torch.optim
as
optim
import
matplotlib.pyplot
as
plt
# 生成一些随机数据
n_samples =
100
data =
torch.randn(n_samples,
2)
# 生成 100
个二维数据点
labels =
(data[:,
0]**2
+ data[:,
1]**2
<
1).float().unsqueeze(1)
# 点在圆内为1,圆外为0
# 可视化数据
plt.scatter(data[:,
0],
data[:,
1],
c=labels.squeeze(),
cmap='coolwarm')
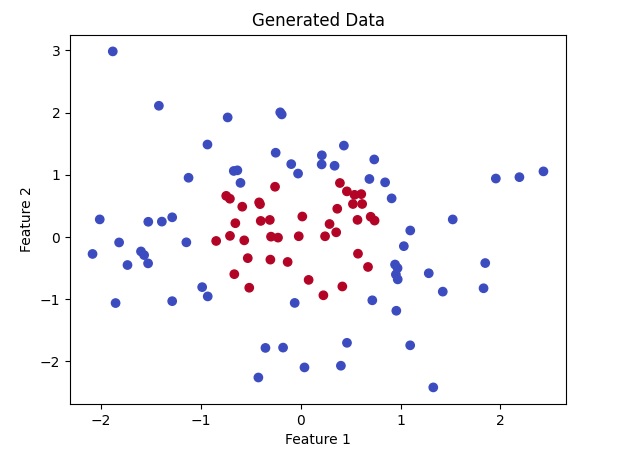
plt.title("Generated
Data")
plt.xlabel("Feature
1")
plt.ylabel("Feature
2")
plt.show()
|
数据说明:
- data 是输入的二维点,每个点有两个特征。
- labels 是目标分类,点在圆形区域内为 1,否则为 0。
显示如下:
2、定义神经网络
用 PyTorch 创建一个简单的前馈神经网络。
前馈神经网络使用了一层隐藏层,通过简单的线性变换和激活函数捕获数据的非线性模式。
|
class SimpleNN(nn.Module):
def __init__(self):
super(SimpleNN, self).__init__()
# 定义神经网络的层
self.fc1 = nn.Linear(2, 4) # 输入层有 2 个特征,隐藏层有 4 个神经元
self.fc2 = nn.Linear(4, 1) # 隐藏层输出到 1 个神经元(用于二分类)
self.sigmoid = nn.Sigmoid() # 二分类激活函数
def forward(self, x):
x = torch.relu(self.fc1(x)) # 使用 ReLU 激活函数
x = self.sigmoid(self.fc2(x)) # 输出层使用 Sigmoid 激活函数
return x
# 实例化模型
model = SimpleNN()
|
3、定义损失函数和优化器
|
# 定义二分类的损失函数和优化器
criterion = nn.BCELoss() # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1) # 使用随机梯度下降优化器
|
4、训练模型
用数据训练模型,让它学会分类。
|
# 训练
epochs = 100
for epoch in range(epochs):
# 前向传播
outputs = model(data)
loss = criterion(outputs, labels)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 每 10 轮打印一次损失
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')
|
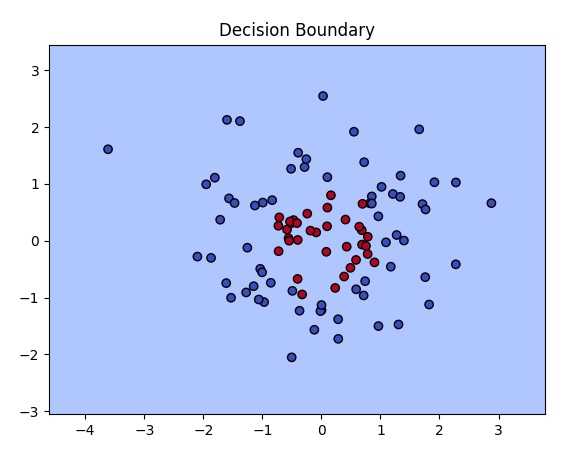
5、测试模型并可视化结果
我们测试模型,并在图像上绘制决策边界。
|
# 可视化决策边界
def plot_decision_boundary(model, data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')
grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
predictions = model(grid).detach().numpy().reshape(xx.shape)
plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
plt.title("Decision Boundary")
plt.show()
plot_decision_boundary(model, data)
|
6、完整代码
完整代码如下:
|
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 生成一些随机数据
n_samples = 100
data = torch.randn(n_samples, 2) # 生成 100 个二维数据点
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1) # 点在圆内为1,圆外为0
# 可视化数据
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
# 定义前馈神经网络
class SimpleNN(nn.Module):
def __init__(self):
super(SimpleNN, self).__init__()
# 定义神经网络的层
self.fc1 = nn.Linear(2, 4) # 输入层有 2 个特征,隐藏层有 4 个神经元
self.fc2 = nn.Linear(4, 1) # 隐藏层输出到 1 个神经元(用于二分类)
self.sigmoid = nn.Sigmoid() # 二分类激活函数
def forward(self, x):
x = torch.relu(self.fc1(x)) # 使用 ReLU 激活函数
x = self.sigmoid(self.fc2(x)) # 输出层使用 Sigmoid 激活函数
return x
# 实例化模型
model = SimpleNN()
# 定义损失函数和优化器
criterion = nn.BCELoss() # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1) # 使用随机梯度下降优化器
# 训练
epochs = 100
for epoch in range(epochs):
# 前向传播
outputs = model(data)
loss = criterion(outputs, labels)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 每 10 轮打印一次损失
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')
# 可视化决策边界
def plot_decision_boundary(model, data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')
grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
predictions = model(grid).detach().numpy().reshape(xx.shape)
plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
plt.title("Decision Boundary")
plt.show()
plot_decision_boundary(model, data)
|
训练时的损失输出:
Epoch [10/100], Loss: 0.5247
Epoch [20/100], Loss: 0.3142
...
Epoch [100/100], Loss: 0.0957
|
图中显示了原始数据点(红色和蓝色),以及模型学习到的分类边界。
|
