| 搭建python环境
windows下可以安装 enthought 集成的 EPDFree32安装包安装python用这个集成了基本所有需要的插件和环境.
装完以后可以运行桌面上pylab程序进入python环境。这个交互环境有点类似于matlab,我们可以快速在上面玩一下python。
做的练习参考下面:
注意: In[n] 的部分是你需要输入的, Out[n] 的部分是系统输出的。
如果安装的是anaconda 版本, 可以选择运行QTconsole 但是注意要先导入几个库函数:
#作图函数
在qtconsole 中用:
%matplotlib inline
否则导入使用:
import matplotlib.pyplot as plt
import pylab as py
import math as m
import scipy.stats as stats
import numpy as np
import pandas as pd |
2的1000次方是多少?
In
[3]: 2 ** 1000
Out[3]: 1071508607186267320948425049060001810561
40481170553360744375038837035105
112493612249319837881569585812759467291755314682
51871452856923140435984577574698
574803934567774824230985421074605062371141877954
18215304647498358194126739876755
916554394607706291457119647768654216766042983165
2624386837205668069376L |
2的100万次方有多少位?
In
[7]: len(str(2**1000000))
Out[7]: 301030 |
2的100万次方里面有多少个0?
import
collections
collections.Counter(str(2**1000000)).most_common()
[('1', 30354),
('4', 30230),
('3', 30193),
('0', 30186),
('5', 30174),
('6', 30103),
('2', 30047),
('9', 30007),
('8', 29896),
('7', 29840)] |
2的100万次方的所有数字之和为多少?
c
= collections.Counter(str(2**1000000)).most_common()
In [9]: sum([i[1] for i in c])
Out[9]: 301030
#总数有301030位
In [10]: sum([i[1]*int(i[0]) for i in c])
Out[10]: 1351546
In [12]: sum([int(i) for i in str(2**1000000)])
Out[12]: 1351546
#数字之和为1351546
#引入字典概念
In [15]: dict(c).values()
Out[15]: dict_values([30103, 30047, 30354,
30186, 30193, 30174, 29840, 30007, 30230,
29896])
In [16]: sum(dict(c).values())
Out[16]: 301030 |
1-1000的所有数字之和为多少?
s=0
for i in range(1,1001):
for j in str(i):
s=s+int(j)
s
Out[16]: 13501
sum(map(int, ''.join(map(str, range(1,
1001)))))
Out[19]: 13501 |
强大的数值运算功能
直接通过公式 pi = 4(1/1 - 1/3 + 1/5
-1/7 +1/9 - 1/11…) 计算π
import
numpy as np
n=1000000
np.sum(4.0/ np.r_[1:n:4, -3:-n:-4])
Out[15]: 3.1415906535897911 |
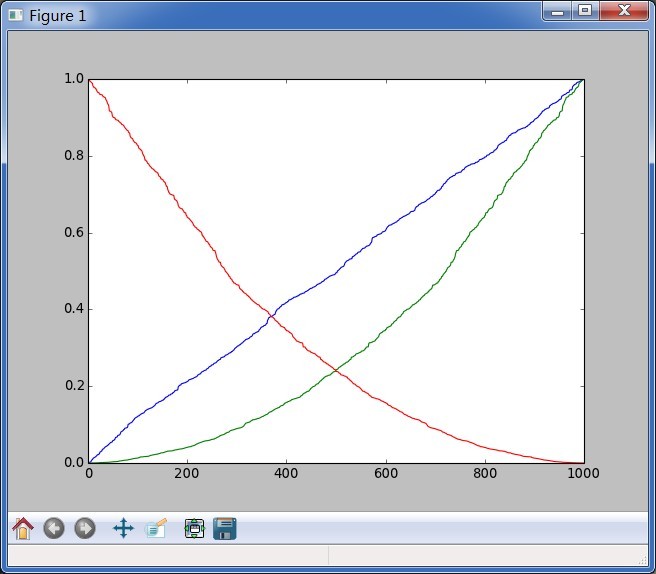
生成1000个0-1的随机数并排序后作图
In
[11]: list = [random.random() for i in range(1000)
]
In [12]: plot(list)
Out[12]: [<matplotlib.lines.Line2D at
0xc9a8370>]
In [13]: plot(sorted(list))
Out[13]: [<matplotlib.lines.Line2D at
0xca46450>] |
如何生成平方数并排序作图?倒序呢?
In
[14]: list = [random.random()**2 for i in
range(1000) ]
In [15]: plot(sorted(list))
Out[15]: [<matplotlib.lines.Line2D at
0xcd65510>]
In [16]: list.sort()
In [17]: list.reverse()
In [18]: plot(list)
Out[18]: [<matplotlib.lines.Line2D at
0xcd720b0>] |
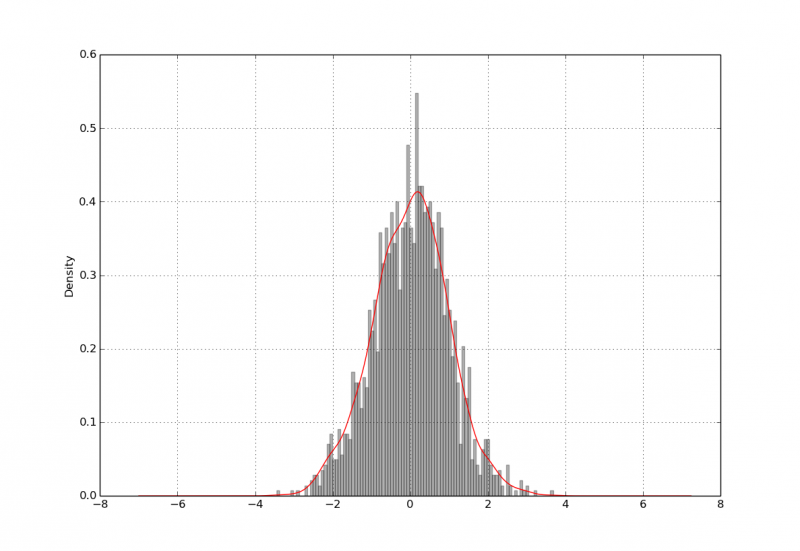
正态分布。。。以及拟合。。。
In
[1]: import numpy as np; import pandas as
pd
In [2]: values = pd.Series(np.random.normal(0,
1, size = 2000))
In [3]: values.hist(bins=100, alpha=0.3, color='k',
normed= True)
Out[3]: <matplotlib.axes.AxesSubplot at
0x7325410>
In [4]: values.plot(kind='kde', style='r-')
Out[4]: <matplotlib.axes.AxesSubplot at
0x7325410> |
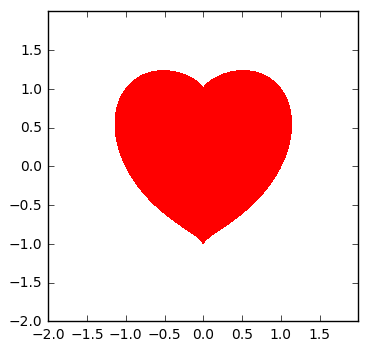
绘图与可视化
通过隐函数(x^2+y^2-1)^3 - x^2 * y^3
=0 绘图
x,
y=np.mgrid[-2:2:500j, -2:2:500j]
z=(x**2 + y**2 -1 )**3 -x**2 * y**3
plt.contourf(x,y,z, levels=[-1,0], colors=["red"])
plt.gca().set_aspect("equal")
plt.show() |
|
